Esplorazione di Min Heap e Max Heap: Fondamenti, Proprietà e Applicazioni

Gli heap sono una pietra miliare dell’informatica, offrendo un modo efficiente per gestire insiemi di dati in continua evoluzione in cui è richiesto un rapido accesso all’elemento minimo o massimo. In questo articolo, esamineremo sia i min heap che i max heap, esplorando le loro definizioni, proprietà, operazioni e applicazioni pratiche.

Cos’è un Heap?

Un heap è una struttura dati ad albero specializzata che soddisfa la proprietà di heap. In un heap, l’albero è sempre completo, il che significa che tutti i livelli sono completamente riempiti tranne possibilmente l’ultimo, che viene riempito da sinistra a destra. Questa natura bilanciata garantisce che le operazioni rimangano efficienti.

• Min Heap: Ogni nodo genitore è minore o uguale ai suoi nodi figli. L’elemento più piccolo si trova sempre alla radice.
• Max Heap: Ogni nodo genitore è maggiore o uguale ai suoi nodi figli. L’elemento più grande si trova sempre alla radice.

Queste proprietà non solo mantengono una struttura parzialmente ordinata, ma rendono anche gli heap ideali per le implementazioni di code a priorità.

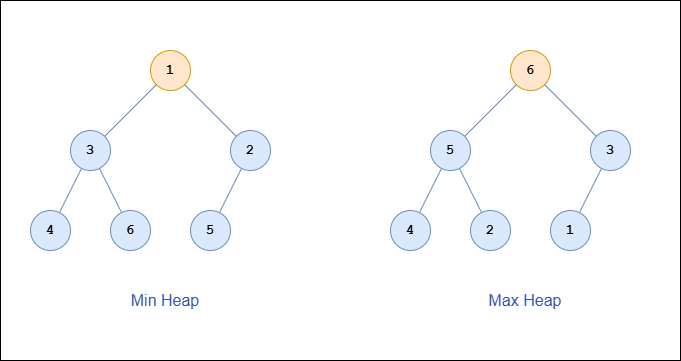
Proprietà e Invarianti degli Heap

La Struttura dell’Albero Binario Completo

Gli heap sono comunemente rappresentati come array. Ciò è possibile perché un albero binario completo non ha lacune e la relazione tra gli indici di genitori e figli può essere calcolata direttamente:

• Parent Index: Per qualsiasi elemento all’indice i, il genitore si trova all’indice Math.floor((i - 1) / 2).
• Child Indices: Il figlio sinistro si trova a 2*i + 1 e il figlio destro a 2*i + 2.

Questa rappresentazione porta a un utilizzo efficiente della memoria e semplifica molte operazioni sugli heap.

Mantenimento della Proprietà di Heap

Sia i min heap che i max heap si basano su procedure di “bubble up” e “bubble down” per mantenere il loro ordinamento dopo inserimenti e rimozioni. Queste operazioni sono fondamentali per garantire che, indipendentemente dalle modifiche, la radice rimanga il più piccolo (in un min heap) o il più grande (in un max heap).

Applicazioni di Min e Max Heap

Code a Priorità

Una delle applicazioni più comuni degli heap è nelle code a priorità, dove gli elementi vengono serviti in base alla priorità anziché al semplice ordine di arrivo. Un min heap è tipicamente utilizzato quando i valori più bassi rappresentano priorità più alte, mentre un max heap è ideale quando i valori più alti indicano una priorità maggiore.

Algoritmi sui Grafi

Algoritmi come il Percorso Minimo di Dijkstra si basano su min heap per selezionare in modo efficiente il prossimo vertice con la distanza provvisoria minima. L’efficienza della struttura contribuisce direttamente alle prestazioni complessive di tali algoritmi.

Ordinamento (Heapsort)

Gli heap possono essere utilizzati per ordinare un array attraverso un processo chiamato heapsort. Convertendo l’array in un max heap ed estraendo ripetutamente l’elemento massimo, si ottiene una sequenza ordinata.

Sistemi in Tempo Reale

In scenari come la pianificazione di attività o la gestione di eventi nei sistemi di simulazione, i tempi di inserimento e rimozione rapidi offerti dagli heap aiutano a mantenere le prestazioni anche quando le priorità cambiano dinamicamente.

Trovare i valori Mediani nei Flussi di Dati

Una strategia comune per trovare la mediana in un flusso di numeri implica il mantenimento di due heap: un min heap per la metà più grande dei dati e un max heap per la metà più piccola. Questo approccio a doppio heap consente un recupero efficiente della mediana anche con l’arrivo di nuovi numeri.

Vantaggi e Limitazioni

Vantaggi

• Efficienza: Gli heap offrono prestazioni O(log n) per inserimento e rimozione, rendendoli molto efficaci per dati in continua evoluzione.
• Semplicità di Implementazione: La loro rappresentazione basata su array semplifica la gestione della memoria.
• Versatilità: Gli heap fungono da spina dorsale per diversi algoritmi e strutture dati importanti, come le code a priorità e l’heapsort.

Limitazioni

• Ordine Parziale: Gli heap non forniscono un ordine completamente ordinato; solo l’elemento estremo (min o max) è garantito nella posizione corretta.
• Efficienza della Ricerca: Sebbene gli heap siano eccellenti per accedere all’elemento radice, la ricerca di elementi arbitrari non è efficiente rispetto ad altre strutture dati come gli alberi di ricerca binari bilanciati.

Considerazioni Avanzate

Varianti di Heap

Oltre ai min e max heap di base, esistono varianti avanzate come i Fibonacci heap e i binomial heap, che offrono complessità temporali ammortizzate migliorate per determinate operazioni. Queste strutture sono particolarmente utili in algoritmi complessi in cui le prestazioni sono critiche.

Complessità di Memoria e Spazio

Gli heap utilizzano memoria contigua quando sono rappresentati come array, rendendoli adatti alla cache. Tuttavia, la semplicità della struttura dell’heap significa che mancano della flessibilità di altre strutture dati quando si tratta di operazioni come l’eliminazione arbitraria di elementi o la ricerca.

Confronto tra Heap e Altre Strutture Dati

Sebbene gli heap eccellano in scenari specifici, non sono una soluzione universale. Ad esempio, gli alberi di ricerca binari bilanciati (come gli alberi AVL o Red-Black) offrono tempi di ricerca più rapidi al costo di implementazioni leggermente più complesse. La scelta tra queste strutture dipende dalle esigenze specifiche dell’applicazione.

Conclusione

I Min e Max Heap sono strutture dati fondamentali con applicazioni diffuse in vari ambiti dell’informatica. La loro efficienza nella gestione delle code a priorità, nel supportare algoritmi sui grafi e nell’abilitare l’elaborazione dei dati in tempo reale li rende strumenti indispensabili nel toolkit di un programmatore. Comprendendo sia i principi generali che i dettagli intricati delle operazioni sugli heap, gli sviluppatori possono prendere decisioni informate su quando e come utilizzare queste strutture nelle loro applicazioni.

Questa combinazione di intuizioni generali ed esame dettagliato sottolinea la versatilità degli heap: che tu stia implementando una coda a priorità di base o ottimizzando algoritmi complessi, gli heap offrono una soluzione robusta che resiste alla prova del tempo.